TFQA: Tools for Quantitative Archaeology - Statistical Analysis Software for Archaeology TFQA
TFQA Logo

TFQA: Tools for Quantitative Archaeology
     kintigh@tfqa.com   +1 (505) 395-7979

TFQA Home
TFQA Documentation
TFQA Orders
Kintigh (ASU Directory)

Rarefy: Rarefaction Diversity Analysis

Performs rarefaction analysis for sets of sample counts in a CSV file, as described by Baxter (2001). Provides expected richness, the standard deviation of the expected richness as well as the Z score and probability for each larger sample rarefied to every smaller sample size. Also outputs expected richness for each sample up to its sample size for graphing. (An additional program, Rarefy_1.exe, is provided if you wish to get results on the rarefaction of only a single sample.  That program is not separately documented but the operation should be self-evident.)

Rarefy is a Windows program written in Delphi, an extension of Pascal as implemented in the Embarcadero RAD Studio XE. 

Running the program

Important information on TFQA programs may be found at http://tfqa.com. See especially, Program Conventions and  Running TFQA under Windows. To run the program, copy Rarefy.exe to a directory that includes the input data files you wish to evaluate (in CSV Format, as described below). Having navigated to that folder, when you double click on Rarefy.exe the program opens a Windows "Run" Window . The program will prompt you for information that it needs to run. Default answers are provided in {curly braces} and can be obtained by just pressing Enter. Reply Y or N to yes or no questions.

Sample Input file (conkey.csv)

The program looks for input in a .csv file. Each case is represented by a single line with a set of counts for the different classes. The first line of the file can be a set of column labels separated by commas (as normally interpreted in CSV files), or the first line can start with the counts. If there is no label line, the program will simply use sequential input case numbers. Case or variable labels with embedded blanks or special characters must be enclosed in quotes (e.g., "variable name"). All numeric variables are assumed to be counts. The sample input file reproduced below is abbreviated, as indicated by the ... ellipsis.

Rarification of a given sample provides expected richness values for smaller sample sizes.  Usually, the observed distribution of counts of a larger sample is used to generate expectations for all smaller sample sizes.  However, in some cases, it may also make sense to generate expectations from either the the combined counts of all observed samples or from a hypothetical sample with (large) counts dictated by a theoretical distribution.  In these latter cases, once can just add one or more observations to the input data set with the desired sets of counts.  These additional observations will not affect the program's calculation of expectations between observed samples. However, if an MDS is performed, the combined sample will affect the results.  

Site,V1,V2,V3,V4,V5,...,V57
Alta/Altamira,2,12,7,1,0,...0
"Mina/Cueto de la Mina",1,12,2,0,1,...,0
"Cier/El Cierro",0,5,1,2,0,...,0
"Juyo/El Juyo",0,8,2,1,0,0,...,0
"Palo/La Paloma",0,4,0,0,0,...,0
Sequence of Program Prompts 
                 +------------------------------------------+
                 ¦               Rarefy V3.0                ¦
                 ¦ Compute Rarefaction Diversity Statistics ¦
                 ¦                                          ¦
                 ¦      (C) 1986-2020 Keith W. Kintigh      ¦
                 ¦           All Rights Reserved            ¦
                 ¦                                          ¦
                 ¦           421 Calle Kokopelli            ¦
                 ¦            Santa Fe, NM 87501            ¦
                 +------------------------------------------+

File of Input Frequencies {.CSV} ? conkey
File: CONKEY.CSV
  First line interpreted as labels for 58 variables:
5   obs & 58 vars; 57 numeric & 1 string
File Variables:
 1"Site   2=V1     3=V2     4=V3     5=V4     6=V5     7=V6     8=V7
 9=V8    10=V9    11=V10   12=V11   13=V12   14=V13   15=V14   16=V15
...
57=V56   58=V57
Variable Number of Default Case Label (Reply 0 for case Number) {0} ? 1

The program asks for the input file name and reports the number of observations and variables and the variable labels (generated if none are provided). The program then asks which variable should be used as a case label. Other non-numeric variables are ignored.

Note: Sample Sizes Range from 23 to 152 Total: 332
Note: Richnesses Range from 12 to 38

Report on the program input.

Printed Analysis Output File (CON for console) {CONKEY.TXT} ?
File Exists; OK to Erase It {N} ? y
CONKEY.TXT Erased
  Analysis Title for Output ? Conkey: Engraved Bone Designs
  Output Line Width (in characters) {120} ? 90
  Print Length for Observation Labels {12} ? 4
  Print Z Score and Probability Matrices in [T]riangular or [S]quare Form {S} ?
  Number of Decimals in Printed Output {3} ?

  Print Input Data Set (Sorted by Sample Size) {Y} ?

The program then asks a series of questions about the output: the output file name, descriptive title, line length (triangular matrices will be easier to read with longer line lengths), the number of characters to use in the printed observation labels, and the number of decimals printed. The label variable in the input dataset may have, long, descriptive labels for the observations.  However, only the specified number of leading characters will be printed. Thus, the label value "Palo/La Paloma" will be printed only as "Palo" if 4 characters is specified as the printed length of the observation labels.  The maximum length that can be printed for an observation label is 12.  The program also asks if you would like the distance matrix output in (lower) triangular or square form and if you would like the input data printed to the output file. 

Phase 1 Computation Begins
  100% Complete
Phase 1 Computation Ends
Phase 1 Compute Time:    0.0 Seconds

Report on the program progress.

Write Triangular Matrix of Probabilities for Analysis in R {Y} ? y
Output File for Distance Matrix {CONKEY.DST} ?
File Exists; OK to Erase It {N} ? y
CONKEY.DST Erased

The program asks if you would like the output probability matrix saved in a file for additional analysis (e.g. via multidimensional scaling in R).

Write Expected Richness Values for SS of 1 to N for Each Case {Y} ?
Output File for Distance Matrix {CONKEY_P.CSV} ?
Maximum Sample Size Plotted {69} ?

Finally the program asks if you would like to calculate and save the expected richness and standard deviations for each case, for sample sizes of 1 to the sample size of the case. By default, for the case with the largest sample size the calculations are only done up to the sample size of the case with the next largest sample size (as that is as far as the comparison can go).

Phase 2 Computation Begins
Phase 2 Computation Ends
Phase 2 Compute Time:    0.3 Seconds

Report on the program progress.

Program End.
OK to Close Program Window {Y} ?

The program provides this prompt to allow you to examine the on-screen results. One you reply with Y or Enter it will close that window and you won’t be able to recover it.

Sample Output Text File

Input Table
     COLUMN...
 ROW      V1      V2      V3      V4      V5      V6      V7      V8      V9     V10
         V11     V12     V13     V14     V15     V16     V17     V18     V19     V20
         V21     V22     V23     V24     V25     V26     V27     V28     V29     V30
         V31     V32     V33     V34     V35     V36     V37     V38     V39     V40
         V41     V42     V43     V44     V45     V46     V47     V48     V49     V50
         V51     V52     V53     V54     V55     V56     V57     Sum    Rich
Palo       0       4       0       0       0       0       0       1       2       2
           0       0       3       0       0       0       0       1       0       0
           0       0       0       0       1       0       0       0       0       0
           0       0       0       0       0       0       0       0       0       0
           0       0       1       0       0       0       0       1       0       0
           0       4       1       0       2       0       0      23      12

...<abbreviated here>
 Sum       3      41      12       4       1       3      12      38       9      21
           2       2      25      11       7      11       3       4      12       6
           5       4       7       1       8       1       2       4       2       2
           1       1       0       7       2       1       1       0       3       0
           1       0       6       0       0       0       3       9       0       0
           0      17      10       0       7       0       0     332

The program first reproduces the input data, with the cases sorted in order of increasing sample size. This ordering creates clarity in the triangular distance matrices produced below. Using this order, the rows in the lower triangular matrix always have the larger sample sizes (on which the rarefaction calculations are done) and the columns in the lower triangular matrix represent the smaller samples. 

Conkey: Engraved Bone Designs
Output Index
Larger
Sample (lower triangular matrix)
Palo:         1    2    3    4
Cier:    1         5    6    7
Juyo:    2    5         8    9
Mina:    3    6    8        10
Alta:    4    7    9   10
      Palo Cier Juyo Mina Alta
       Smaller Sample (lower triangular matrix)

The program results are provided in a list mode and are summarized in triangular matrices. The Output Index Matrix, above, indicates the place in the list output (which follows) in which the relevant result is found. 

     | Larger Sample      | Smaller Sample
Indx | Case   SS Richness | Case   SS Rich(obs) Rich(exp) StdDev ZScore  Prob
   1 | Cier   35       15 | Palo   23        12    12.343  1.145 -0.299 0.382
   2 | Juyo   53       19 | Palo   23        12    11.720  1.547  0.181 0.428
   3 | Mina   69       27 | Palo   23        12    14.475  1.667 -1.485 0.069
   4 | Alta  152       38 | Palo   23        12    15.434  1.742 -1.971 0.024
   5 | Juyo   53       19 | Cier   35        15    15.090  1.412 -0.064 0.475
   6 | Mina   69       27 | Cier   35        15    18.783  1.740 -2.174 0.015
   7 | Alta  152       38 | Cier   35        15    19.980  2.003 -2.486 0.006
   8 | Mina   69       27 | Juyo   53        19    23.653  1.412 -3.294 0.000
   9 | Alta  152       38 | Juyo   53        19    24.901  2.102 -2.807 0.003
  10 | Alta  152       38 | Mina   69        27    28.158  2.054 -0.564 0.286

Each result line shows the larger sample size case whose counts--when rarefied--produce an expectation for the richness (and its standard deviation) for the sample size of the smaller sample size case. Then, using the observed richness of the smaller sample size case, a Z score is produced, indicating how many standard deviations the observed richness is above (+) or below (-) the expected (rarefied) richness. Finally a one-tailed normal probability is calculated for that Z score. A low probability indicates that it is unlikely the the observed richness would occur by chance for the smaller sample size. The Z score indicate whether the observed richness for the smaller sample is too high (+) or too low (-).

Conkey: Engraved Bone Designs
Z Score
Larger
Sample (lower triangular matrix)
Palo:        -0.299  0.181 -1.485 -1.971
Cier: -0.299        -0.064 -2.174 -2.486
Juyo:  0.181 -0.064        -3.294 -2.807
Mina: -1.485 -2.174 -3.294        -0.564
Alta: -1.971 -2.486 -2.807 -0.564
        Palo   Cier   Juyo   Mina   Alta
       Smaller Sample (lower triangular matrix)

Conkey: Engraved Bone Designs
Normal Probability
Larger
Sample (lower triangular matrix)
Palo:       0.382 0.428 0.069 0.024
Cier: 0.382       0.475 0.015 0.006
Juyo: 0.428 0.475       0.000 0.003
Mina: 0.069 0.015 0.000       0.286
Alta: 0.024 0.006 0.003 0.286
       Palo  Cier  Juyo  Mina  Alta
       Smaller Sample (lower triangular matrix)

The list mode results for Z score and probability are printed in triangular matrix form.

Probability Matrix Output for Further Analysis (conkey.dst)

If requested the program outputs a lower triangular of the probabilities for further analysis.

"Palo" "Cier" "Juyo" "Mina" "Alta"
  0.382370
  0.428221   0.474611
  0.068745   0.014842   0.000494
  0.024367   0.006451   0.002501   0.286486

The following R script will perform a 2 dimensional multidimensional scaling of these values. Note that in this script the probabilities are converted to dissimilarities (distances) by subtracting from 1. (A probability near 0 indicates a high level of dissimilarity and a probability near 1.0 a high level of similarity). 

#*********************************
#* MDS of Rarefy Probability *****
#*********************************
library("dplyr")
library("MASS")

filename <- "conkey.dst"
#input file has a line of labels, followed by a lower triangular matrix
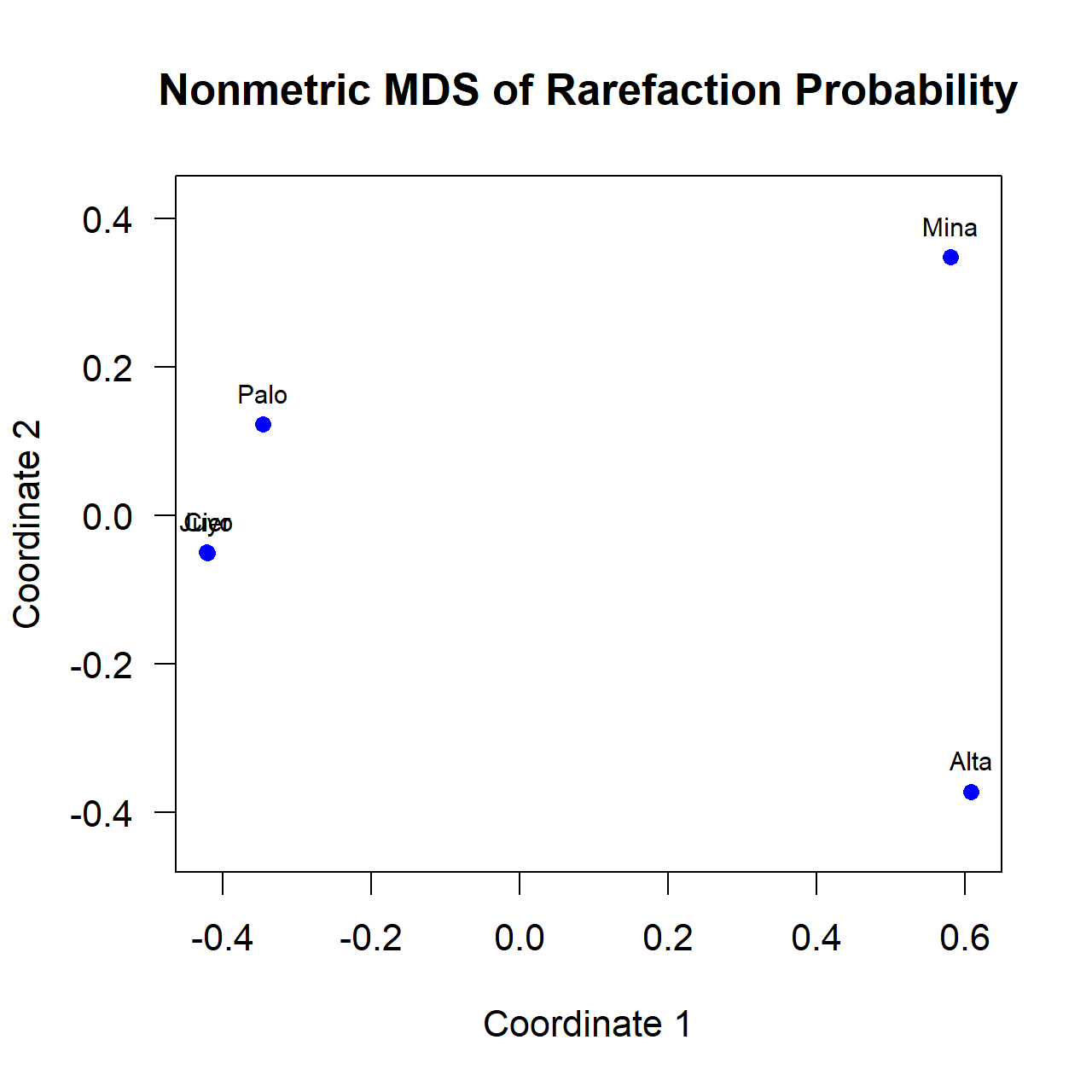
MDS of Conkey Rarefaction Analysis 
olabel <- scan(filename,what="list", nlines=1)
olabel
data <- scan(filename,skip=1)
#data
num_cols <- (1 + sqrt(1 + 8*length(data)))/2 - 1
mat <- matrix(0, num_cols, num_cols)
mat[row(mat) <= col(mat)] <- data
mat <- t(mat)
#mat

#Finally to get a 'dist' object:
#Probabilities converted to distance with 1-p
mat <- rbind(0, mat)
mat <- cbind(mat, 0)
d   <- as.dist(mat)
d <- 1-d
attr(d, "Labels") <- olabel

fit <- isoMDS(d, k=2) # non-Metric (kruskal) MDS
fit # view results

# plot solution
x <- fit$points[,1]
y <- fit$points[,2]
# png("conkeyMDS.png",width=5,height=5,units="in",res=256)
plot(x, y, xlab="Coordinate 1", ylab="Coordinate 2",
     main="Nonmetric MDS of Rarefaction Probability",  pch=16, las=1, asp=1, col="blue")
text(x, y, labels = olabel, cex=.7, pos=3, asp=1)
# dev.off()

Rarefaction Trace Plot Output (conkey_p.csv)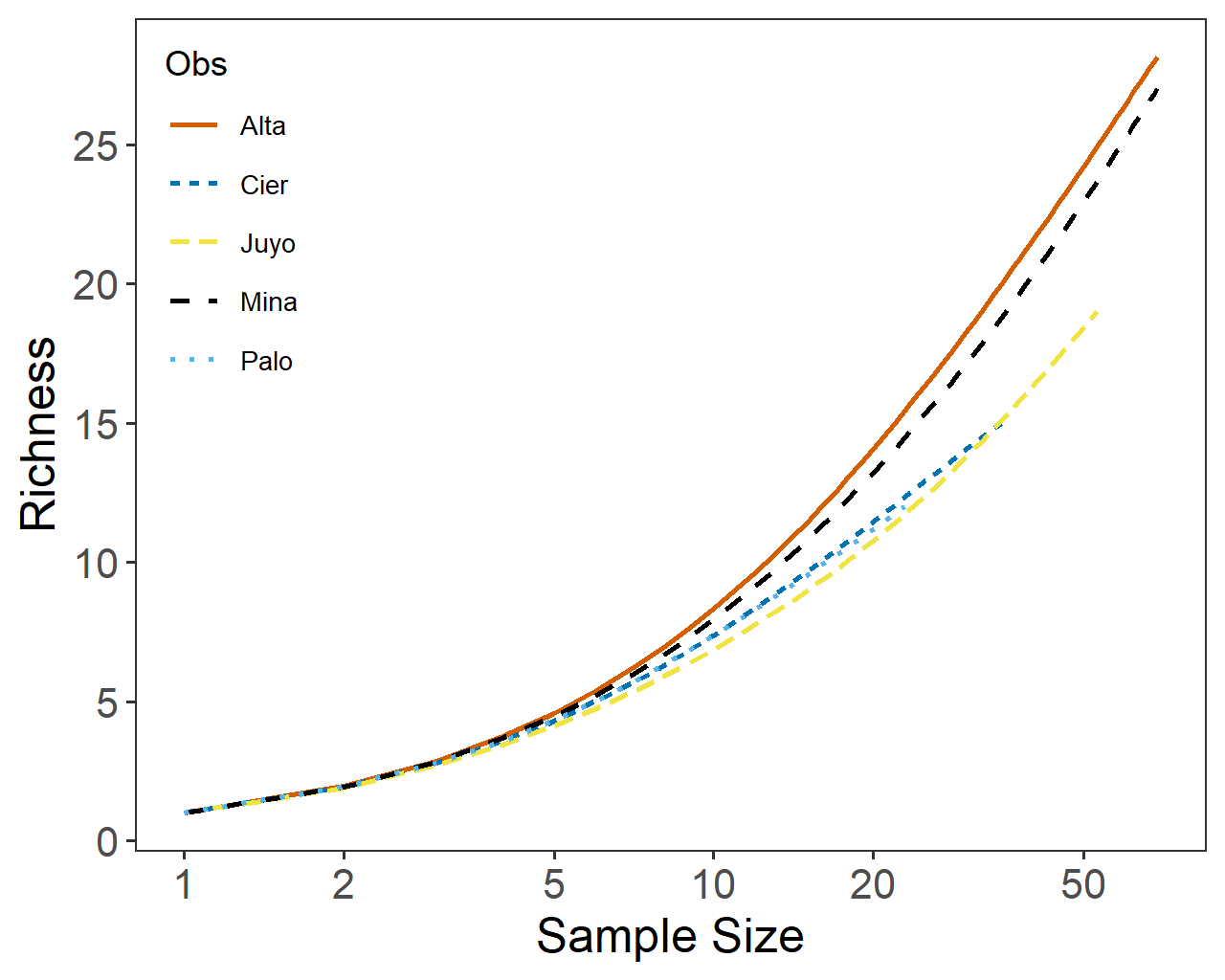

Conkey Rarefaction Analysis 
Obs,SS,Richness,Std
"Palo",1,1.00,0.00
"Palo",2,1.93,0.26
"Palo",3,2.79,0.42
...
"Palo",22,11.74,0.44
"Palo",23,12.00,0.00
"Cier",1,1.00,0.00
"Cier",2,1.92,0.26
...
"Cier",35,15.00,0.00
"Juyo",1,1.00,0.00
"Juyo",2,1.90,0.30
...
"Juyo",53,19.00,0.00
"Mina",1,1.00,0.00"Mina",2,1.94,0.23
...
"Mina",69,27.00,0.00
"Alta",1,1.00,0.00
"Alta",2,1.96,0.20
...
"Alta",69,28.16,2.05

The following R code will produce a rarefaction trace from this output file. 

library("ggplot2")
library("plyr")
library("dplyr")

#+++++++++++++++++++++++++++++
#== Rarefaction Trace Plot +++
#+++++++++++++++++++++++++++++

filename <- "conkey_p.csv"
trace <- read.csv(filename)

cbPalette <- c( "#D55E00", "#0072B2", "#F0E442", "#000000", "#56B4E9", "#E69F00", "#009E73", "#CC79A7")

trace <- replace(trace, trace == 0, NA)
trace <- data.frame(trace)

png("conkeyTrace.png",width=5,height=4,units="in",res=256)

ggplot(trace, aes(x=SS, group=Obs, color=Obs, linetype=Obs,)) +
  geom_line(aes(y=Richness), size=0.75) +
#  geom_line(aes(y=Richness-Std), size=0.75) +  # this & next lines add +/- SD line for each case
#  geom_line(aes(y=Richness+Std), size=0.75) +  #
#  scale_x_continuous(name='Sample Size')+       #, limits=c(0,50),breaks=seq(0,50,5)) +  #use instead of next line for linear scale
  scale_x_log10(name='Sample Size'  , breaks=c(1,2,5,10,20,50,100,200,500,1000,2000,5000)) + 
  scale_y_continuous(name='Richness', breaks=seq(0,200,5)) +
  theme_bw() +
  theme(axis.text.x = element_text(size=12),  axis.text.y = element_text(size=12), 
        axis.title.x = element_text(size = 14),axis.title.y = element_text(size = 14),
        panel.grid.major = element_blank(), panel.grid.minor = element_blank())+ 
  
  theme(legend.position = c(0.01,0.99), 
        legend.justification = c(0, 1), 
        legend.text=element_text(size=8), 
        legend.title=element_text(size=10)) +
  scale_colour_manual(values=cbPalette)
dev.off()

References Cited

Baxter, M. J.

2001  Methodological Issues in the Study of Assemblage Diversity. American Antiquity. 66(4): 715-725.

Page Last Updated: 4 Octoberil 2020
Home Top Overview Ordering Documentation