TFQA: Tools for Quantitative Archaeology
     kintigh@tfqa.com   +1 (505) 395-7979

TFQA Home
TFQA Documentation
TFQA Orders
Kintigh(ASU Directory)

BAYES: Bayesian Methods for Proportions

BAYES, while not currently supported or thoroughly documented, is included in the TFQA package for those interested. The program implements Bayesian methods for proportions as described by Iversen (1984). The notation used in prompts and in output follows Iversen. Intervals are calculated and graphed for Bayesian estimates of proportions based on both flat (uninformative) and informative priors. Informative priors can be described by their mean and standard deviation of a Beta distribution.

1984  Bayesian Statistical Inference, Quantitative Applications in the Social Sciences 43, Sage University Papers, Beverly Hills, California.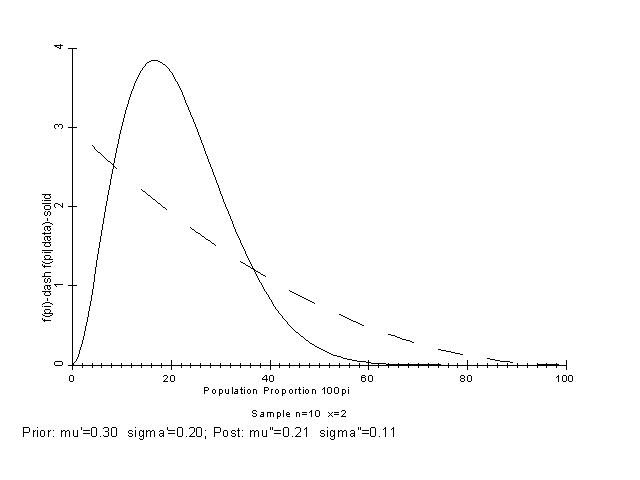

Figure 12. Plot of Bayesian Prior and Posterior Probabilities.

PROGRAM EXAMPLE

Output File Name {CON} ?
Create a Plot for a HPGL Plotter {N} ?

Bayesian Estimates for Proportions
[I]nformative or [F]lat Prior {F} ? I
Prior Beta Distribution µ { 0.000} ? .3
Prior Beta Distribution s { 0.000} ? .2
Sample n {0} ? 10
Sample x {0} ? 2

Sample n =  10  Sample x =   2
Prior a' =   1  Prior b' =   3  C' = 3.000E+00
Post a"  =   3  Post b"  =  11  C" = 8.580E+02
Prior µ' = 0.300  Prior s' = 0.200
Post µ"  = 0.214  Post s"  = 0.106

Print Bayesian Probability Intervals {Y} ? Y
  Resolution of p (.001 - .01) {0.010} ?
Bayesian Probability Intervals
100%

             Tail                         Interval
       ----------------  ------------------------------------------
Level     p0   P(p<=p0)     p1    p2   P(p1<=p<=p2)   f(p1)   f(p2)
 0.01   0.040    0.014    0.170 0.180      0.038      3.847   3.821
 0.05   0.070    0.058    0.160 0.180      0.077      3.842   3.821
 0.10   0.090    0.105    0.150 0.180      0.115      3.801   3.821
 0.20   0.130    0.234    0.140 0.200      0.228      3.722   3.685
 0.25   0.140    0.270    0.130 0.200      0.265      3.602   3.685
 0.50   0.210    0.535    0.100 0.240      0.503      2.992   3.177
 0.75   0.280    0.751    0.070 0.310      0.761      2.035   2.017
 0.80   0.310    0.819    0.060 0.330      0.816      1.664   1.703
 0.90   0.360    0.900    0.040 0.380      0.910      0.913   1.040
 0.95   0.420    0.957    0.030 0.430      0.957      0.569   0.574
 0.99   0.510    0.991    0.000 0.990      1.000      0.000   0.000

Display Plot {Y} ?
Program End